Important update from TheSchoolRun
For the past 13 years, TheSchoolRun has been run by a small team of mums working from home, dedicated to providing quality educational resources to primary school parents. Unfortunately, rising supplier costs and falling revenue have made it impossible for us to continue operating, and we’ve had to make the difficult decision to close. The good news: We’ve arranged for another educational provider to take over many of our resources. These will be hosted on a new portal, where the content will be updated and expanded to support your child’s learning.
What this means for subscribers:
- Your subscription is still active, and for now, you can keep using the website as normal — just log in with your usual details to access all our articles and resources*.
- In a few months, all resources will move to the new portal. You’ll continue to have access there until your subscription ends. We’ll send you full details nearer the time.
- As a thank you for your support, we’ll also be sending you 16 primary school eBooks (worth £108.84) to download and keep.
A few changes to be aware of:
- The Learning Journey weekly email has ended, but your child’s plan will still be updated on your dashboard each Monday. Just log in to see the recommended worksheets.
- The 11+ weekly emails have now ended. We sent you all the remaining emails in the series at the end of March — please check your inbox (and spam folder) if you haven’t seen them. You can also follow the full programme here: 11+ Learning Journey.
If you have any questions, please contact us at [email protected]. Thank you for being part of our journey it’s been a privilege to support your family’s learning.
*If you need to reset your password, it will still work as usual. Please check your spam folder if the reset email doesn’t appear in your inbox.
What are line symmetry, reflective symmetry and rotational symmetry?
What are line symmetry, reflective symmetry and rotational symmetry?
Line symmetry, reflective symmetry and rotational symmetry are different types of symmetry. Symmetry is where something is the same on both sides; then it would be said to be symmetrical.
What is line symmetry?
Shapes or patterns can have multiple lines of symmetry, depending on how many times the shape can be folded in half and still remain the same on both sides.
What is reflective symmetry?
Reflective symmetry is when a shape or pattern is reflected in a line of symmetry / a mirror line. The reflected shape will be exactly the same as the original, the same distance from the mirror line and the same size.
What is rotational symmetry?
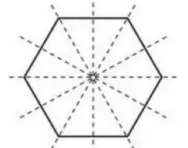
Rotational symmetry is when a shape or pattern can be rotated or turned around a central point and remains the same. It may be stated that a shape has a rotational symmetry of order X; this means that the shape can be turned around a central point and remain the same X times.
When are children taught about different kinds of symmetry in primary school?
In Year 2 children will be introduced to the concept of symmetry and taught to identify line symmetry in a vertical line. They may be given the shapes and asked to fold them or draw on a line of symmetry.
In Year 3 children are taught to sort shapes into symmetrical and non-symmetrical polygons.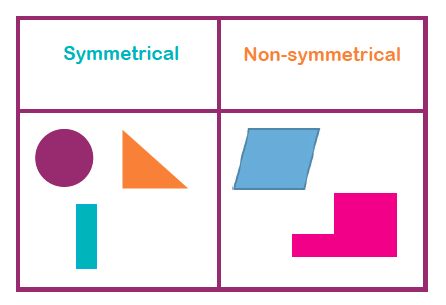
In Year 4 children identify lines of symmetry in 2D shapes. They will become aware that shapes may have more than one line of symmetry and complete investigations about how many lines of symmetry shapes have.
Children will also learn to draw symmetrical patterns with respect to a specific line of symmetry. They will often use squared paper to do this task.
In Year 5 children are taught to reflect shapes and patterns in lines that are parallel to the axis. For example, they may be given half a shape and asked to complete it using the mirror line.
Or they may be asked to reflect whole shapes in a mirror line. 
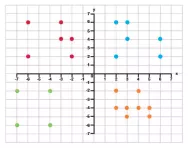
In Year 6 children reflect shapes. They will be given a shape and asked to reflect in the other three quadrants using the x-axis and y-axis. This is often combined with coordinates work.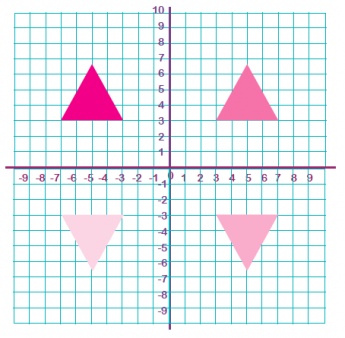
In Year 6 some more able children will also look at rotational symmetry (generally taught in Y7). They will be taught to identify how many times a shape can be rotated around a centre point and remain the same. They will be able to use rotational symmetry when describing a shape's properties.
