Important update from TheSchoolRun
For the past 13 years, TheSchoolRun has been run by a small team of mums working from home, dedicated to providing quality educational resources to primary school parents. Unfortunately, rising supplier costs and falling revenue have made it impossible for us to continue operating, and we’ve had to make the difficult decision to close. The good news: We’ve arranged for another educational provider to take over many of our resources. These will be hosted on a new portal, where the content will be updated and expanded to support your child’s learning.
What this means for subscribers:
- Your subscription is still active, and for now, you can keep using the website as normal — just log in with your usual details to access all our articles and resources*.
- In a few months, all resources will move to the new portal. You’ll continue to have access there until your subscription ends. We’ll send you full details nearer the time.
- As a thank you for your support, we’ll also be sending you 16 primary school eBooks (worth £108.84) to download and keep.
A few changes to be aware of:
- The Learning Journey weekly email has ended, but your child’s plan will still be updated on your dashboard each Monday. Just log in to see the recommended worksheets.
- The 11+ weekly emails have now ended. We sent you all the remaining emails in the series at the end of March — please check your inbox (and spam folder) if you haven’t seen them. You can also follow the full programme here: 11+ Learning Journey.
If you have any questions, please contact us at [email protected]. Thank you for being part of our journey it’s been a privilege to support your family’s learning.
*If you need to reset your password, it will still work as usual. Please check your spam folder if the reset email doesn’t appear in your inbox.
What is 'shared between'?
What is 'shared between'?
'Shared between' is a term used in word problems that involve division. An example of such a Key Stage 1 problem might be:
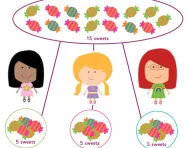
Nathan has 20 sweets. He shares them equally between his four friends. How many sweets does each friend get?
Teachers will often give children counters to work out these problems. They may encourage them to draw stick men to represent the four friends, and then show them how to share the counters equally between the four friends, by giving one to each child until there are none left.
'Sharing' division word problems in primary school
In Year 1, children need to share into groups of 2, 5 or 10 (this coincides with their learning of the 2, 5 and 10 times tables in Key Stage 1).
In Year 2, children would be introduced to various symbols including ÷ and would need to know that this symbol means 'divide' or 'share'.
In Year 3, children may still come across the word 'share' and will be moving onto dividing larger numbers by one-digit numbers, such as 50 ÷ 4.
As children get more confident with their times tables and start to learn how these are related to division, children (especially in Year 3) are encouraged to use the inverse to work out problems like the above one. So instead of sharing 20 counters into 4 equal groups, they realise that the above problem would be written as a number sentence like this:
20 ÷ 4 =
They would then use their knowledge of times tables and the inverse to remember that 4 x 5 = 20, therefore the answer must be 5.
Children in later Key Stage 2 will still come across the word 'share' in their maths problems. In Year 6 children need to be able to mentally divide a decimal by a unit. For example in the following problem:
I have 1.2 litres of orange juice. I need to share this equally between six people. How much orange juice will each child get?
- One way of doing this is to convert the 1.2 litres into 1200ml and then recall that there are 5 lots of 200 in 1000, so there must be six lots of 200 in 1200, therefore each child will get 200ml.
- Another way of doing this is to think of the question as a number sentence: 1.2 ÷ 6 =
- Since a child would know that 12 ÷ 6 is 2, they could then work out that 1.2 ÷ 6 = 0.2, so give their answer as 0.2 litres or 200ml.
Children at this stage should also have efficient methods for dividing larger numbers. For example, they may come across a problem as follows:
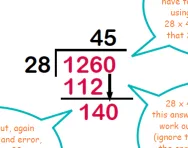
John has 362 marbles in a jar. He shares them between 7 people. How many marbles does each friend get? How many marbles are left over?
Here a child could use the bus stop method:
Or they might choose to think about what they would multiply 7 by to make a number close to 362. They might work out that 5 x 7 = 35, therefore 5 x 71 = 351 with 5 left over, therefore each child would get 51 marbles with 5 left over.